|
Relatives of DFT
Definitions
Formation
Relationship
Mathematic
Relationship
Properties of DFT
Periodical
Convolution Law
Circular Convolution Law
Symmetry
Relatives of DFT
Equations
|
|
Laplace
Transform
|
|
|
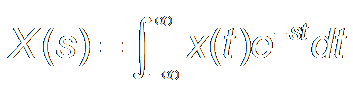
Fourier Transform
|
|
|
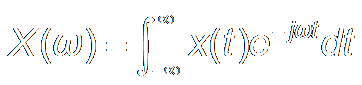
Z Transform
|
|
|
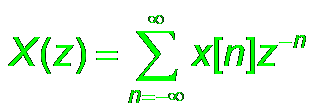
DTFT
|
|
|
|
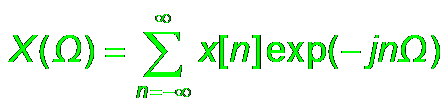
DFS
|
|
|
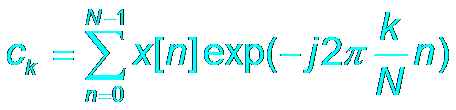
DFT
|
|
|
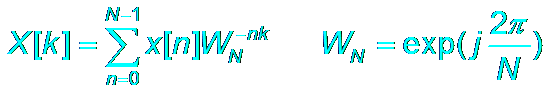
(k = 0, 1, ? N-1)
|
Formation
Relationship
|
LT
|
|
Complex
Exponential
|
s→jω
|
Imaginary
Exponential
|
|
FT
|
|
Time
Continuous
|
ejω→z , t→n
|
Time Discrete
|
|
ZT
|
|
Frequency
Continuous
|
z→ejΩ
|
Frequency
Discrete
|
|
DTFT
|
|
Inf. Time, Cont. Freq.
|
(-∞,∞)→(0,N-1)
Ω→2πk/N
|
Finite Time, Discr. Freq.
|
|
DFS
|
|
Periodic
Signal
|
ck→X[k]
|
Nonperiodic Signal
|
|
DFT
|
Mathematic
Relationship
Laplace &
Z
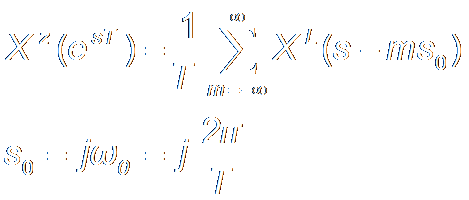
Fourier & Z
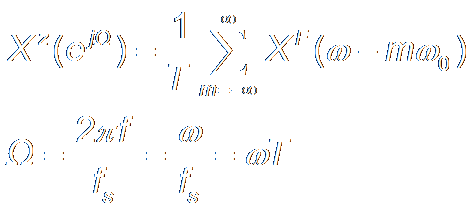
DFT & Z
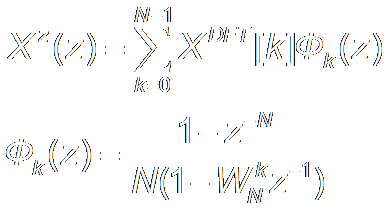
DFT & DTFT
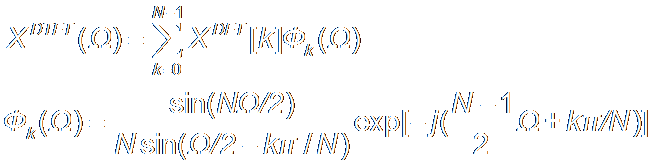
Properties of DFT
Periodical Convolution Law
Given
Periodical Sequences x1[n], x2[n],
x3[n]
with period of N,
DFT of them are X1[k], X2[k],
X3[k].
If X3[k] = X1[k]
X2[k] , then
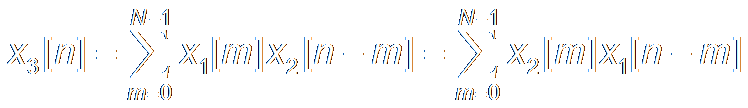
Circular
Convolution Law
Circular Shift ( Non-Periodical x[m] )
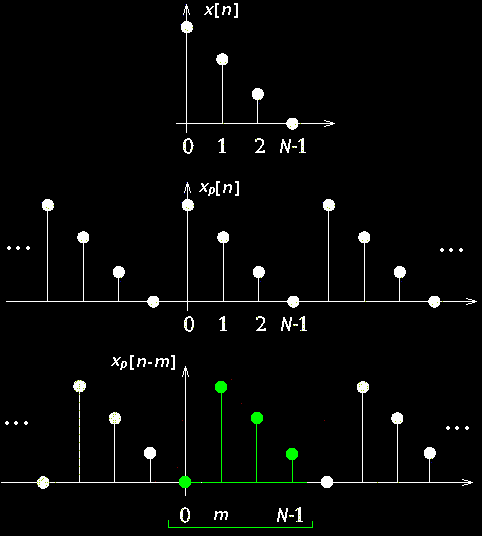
xp[n-m]RN[n]
m
Samples Circular Shift of x[n], where
RN[n] is Rectangular
Window of length N.
Circular Convolution:
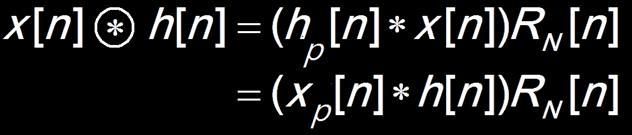
Circular
Convolution Law
Given Finite Length Sequences x[n], h[n], y[n]
with same Length N, DFT of them are X [k],
H [k],
Y [k]. If Y [k] = X [k]
H [k] , then
y[n] = x[n] # h[n]
 :Convolution can be done by DFT !
 :If length of two sequences are M
& N,
one
of them must be expanded into
a (M+N-1)
periodical sequence.
Symmetry
|
Signal
|
DFT
|
|
x[n]
|
X[k]
|
|
x*[n]
|
X* [-k]
|
|
x*
[-n]
|
X*[k]
|
|
Re{ x[n] }
|
Xe[k]
|
|
j Im{ x[n] }
|
Xo[k]
|
|
xe[n]
|
Re{ X[k] }
|
|
xo[n]
|
j Im{ X[k]
}
|
|
X[n]
|
N x[-k]
|
Even Symmetry Sequence:
xe[n] = (
x[n] + x* [-n]
) / 2
Xe[k] = ( X[k] + X* [-k] ) / 2
Odd Symmetry Sequence:
xo[n] = ( x[n] - x* [-n] ) / 2
Xo[k] = ( X[k] - X* [-k] ) / 2
|
