|
|
Derivation引出 of DFT
Definition of DFT
Resolution and
Smearing
分辨率与拖尾
Window Effect &
Spectrogram
窗效应与谱图
Homework
p482:
11.2, p483: 11.6
Derivation引出 of DFT
|
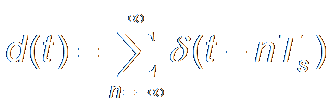
|
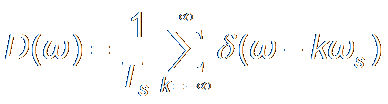
|
|
|
|
|
|
|
|
|
|
|
Time Domain
|
Frequency Domain
|
|
Continuous , Infinite
|
Continuous
, Finite
|
|
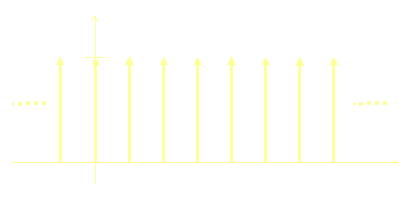
|
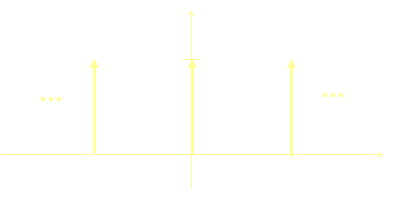
|
|
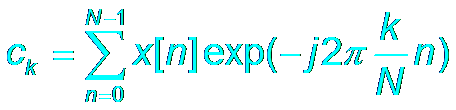
Discrete
, Infinite
|
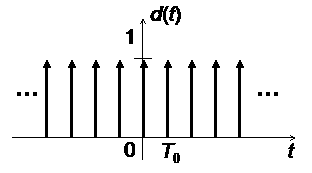
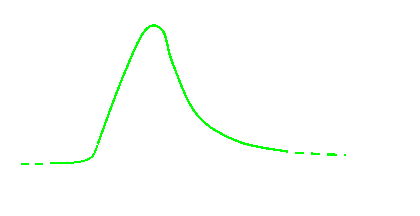
Continuous
, Infinite
|
|
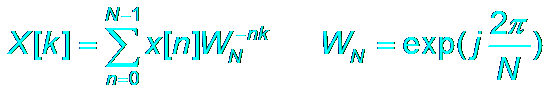
|
|
|
|
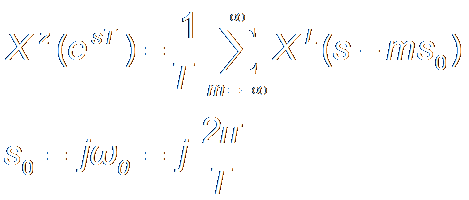
|
|
Discrete
, Infinite
|
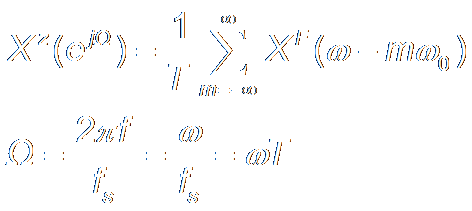
Discrete
, Infinite
|
|
Discrete
, Finite
|
Discrete
, Finite
|
|
|
|
|
|
|
|
Signal
|
Spectrum
Shape
|
|
DFS
|
Periodic,
Finite
|
Unchanged
|
|
DTFT
|
Non-periodic,
Infinite
|
Unchanged
|
|
DFT
|
Non-periodic,
Finite
|
Maybe
unchanged
|
DFT
Definition
Provide:
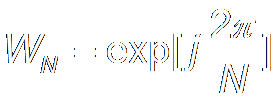
|
DFT:
N-Periodic
|
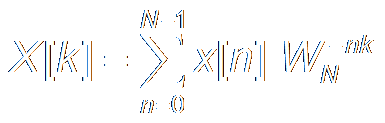
k
= 0, 1, ..., N-1.
|
|
IDFT:
N-Periodic
|
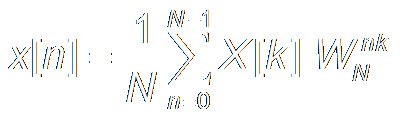
n
= 0, 1, ..., N-1.
|
X[k] = |X[k]| exp( jq [k])
Magnitude
Spectrum: |X[k]|
Phase Spectrum: q [k]
DTFT
Magnitude Spectrum
DFT
Magnitude Spectrum
DTFT and
DFT Magnitude Spectra
Resolution and
Smearing
分辨率与拖尾
|
Spectrum Resolution
|
DFT Frequencies
|
|
Δf = fS
/ N (Hz)
|
fk
= k fS / N (Hz)
k
= 0, 1, ..., N-1
|
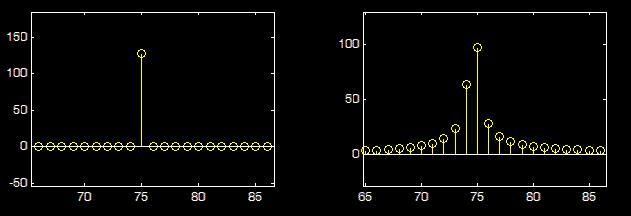
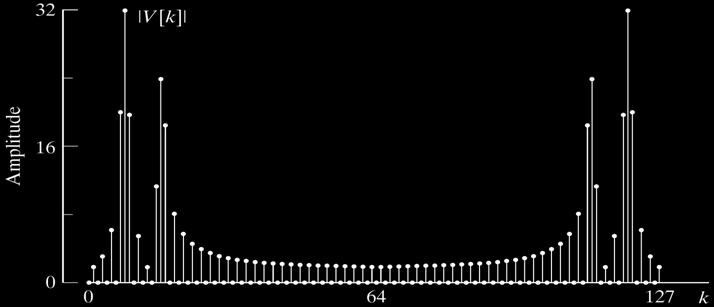
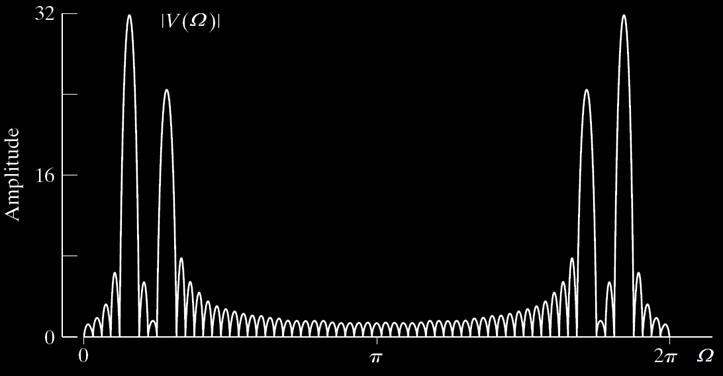
Example of
two sinusoid signals:
fs = 8 kHz, N = 256, Δf =31.25Hz
f1= 2.3125 kHz , f2= 2.3kHz
.
DFT
Frequencies:
f73 = 73(8000/256) = 2281.25 Hz
f74 = 74(8000/256) = 2312.5 Hz
X1[k]
X2[k]
  ? ?
Window Effect & Spectrogram
窗效应与谱图
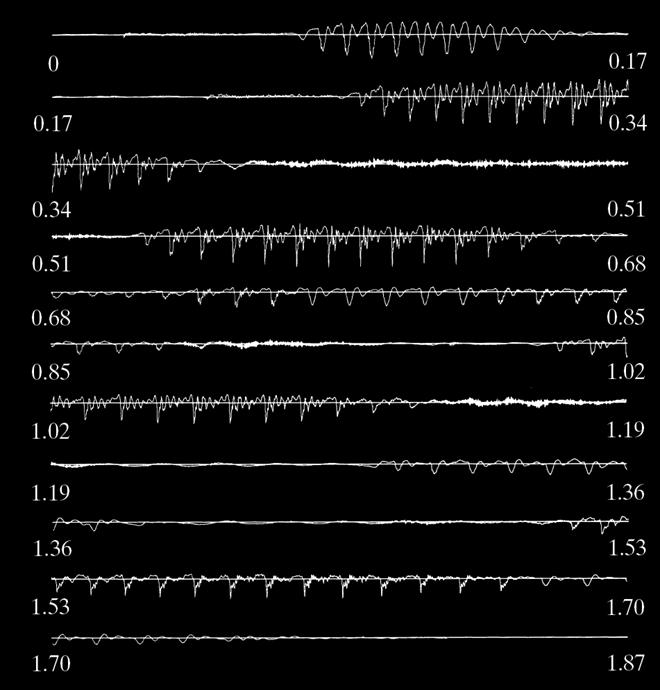
Window
Effect: Time-Frequency Trade-off
Fixed
Sampling Rate:
Long Window v.s. Short Window
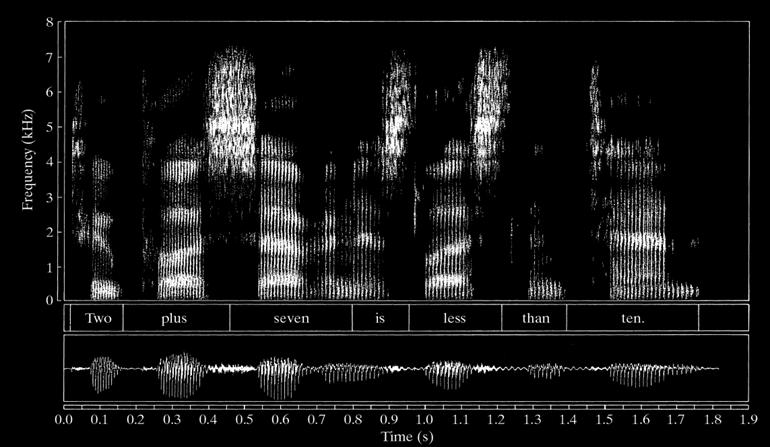
Spectrogram: Short Time Fourier Transform
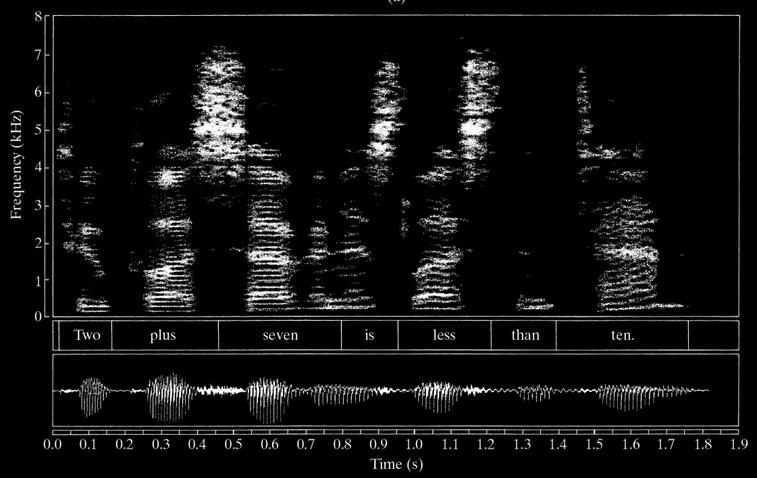
|