Index
			Go Top
Go Top
	Go Top
		Go Top
		Go Top

Approximate An Ideal Low Pass Filter 理想低通滤波器的近似

Windows for FIR Filter Design

FIR滤波器设计用的窗函数

Filter Features 滤波器指标

Steps of Windowed FIR Design 窗函数FIR滤波器设计步骤

Examples

HomeWork: p379: 9.12, p380: 9.25

Approximate Ideal Low Pass Filter

Ideal Low Pass Filter Shape

   Impulse Response of Ideal LPF

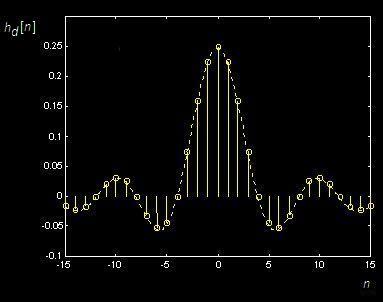
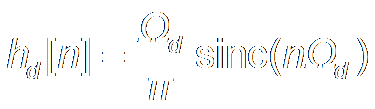
Infinite Length, Non-Casual!

Windowing!

      Rectangular Window

      Its Frequency Response:   

 Multiply h_d [n] with Window w[n]:

h[n] = h_d [n] w[n]

           H(Ω) = H_d(Ω) * W(Ω)

Non-Ideal Low Pass Filter Shape:

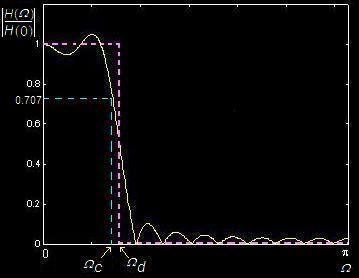
   Cut-off frequency:  Ω_c    

20log|H(Ω_c)|/|H(0)| = 3 dB

  Finite Length in Time,

                  Smearing(拖尾) in Frequency.

Practicability 实用性

Quality 品质

Filter Features

Non-Ideal Low Pass Filter Shape:

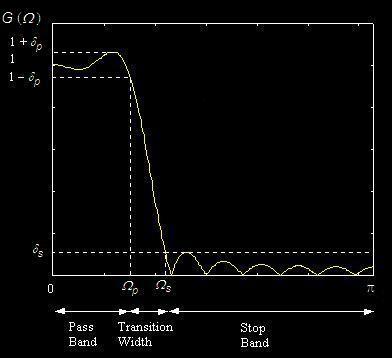
      Pass band edge frequency: Ω_p

_{通带边缘频率}

      Stop band edge frequency: Ω_s

_{阻带边缘频率}

      Transition width: |Ω_s - Ω_p|

_过度带宽

      Pass band ripple: d_p

_通带波纹

      Stop band ripple: d_s

_阻带波纹

      Stop band attenuation:   -20log(d_s)

_阻带衰减

Windows for FIR Filter Design

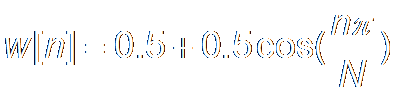
Hanning Window:	|n| ≤ N
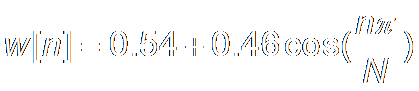
Hamming Window:	|n| ≤ N
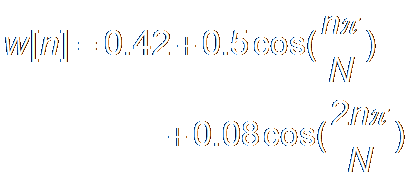
Blackman Window:	|n| ≤ N
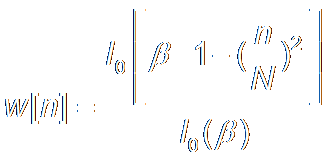
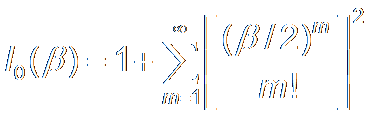
Kaiser Window:	Zero Order Modified Bessel Function 零阶修正贝塞尔函数 |n| ≤ N

Steps of Windowed FIR Design

Low Pass Filter

According to the Given Filter Specification

                { f_pass , f_stop , f_s, d_s }

        ----------------------------------------------------------------------

       1. Set  f_d = (f_pass+ f_stop)/2

       2. Compute

Ωd= 2π fd /fs ,

       3. According to 20log(d_s), From Table 9.3,

           Choose  w[n] and the Filter Length (2N+1) .

4. Calculate impulse response

h[n] = h_d[n]w[n].

5. Shift the h[n] to the right by N samples.

       ------------------------------------------------------------------------

P345, Example 9.7

Band Pass & High Pass Filters

Band Pass Filter { fstop,  fpass, f0, fs, ds}	High Pass Filter { fstop, fpass , fs, ds }
1. fd = f0 - (fpass+ fstop)/2 4. h[n]=hd[n]w[n]cos(nΩ0) Ω0 = 2π f0 / fs	1. fd = fs - (fpass+ fstop)/2 4. h[n]=hd[n]w[n]cos(nπ)

P355, Figure 9.45              P359, Example 9.11

Band Stop = Low Pass + High Pass

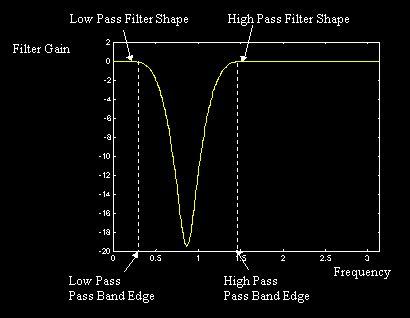
H_BS(Ω) = H_LP(Ω) + H_HP(Ω)

h_BS[n] = h_LP[n] + h_HP[n]

Ω_p^LP < Ω_p^HP

Band Pass = Low Pass x High Pass

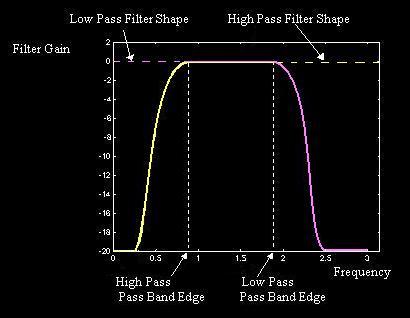
H_BP(Ω) = H_LP(Ω) H_HP(Ω)

h_BP[n] = h_LP[n] * h_HP[n]

Ω_p^LP > Ω_p^HP

.

Examples

Filtering Speech

Original     Low Pass Filtering      High Pass Filtering

Filtering Music

Original     Low Pass Filtering