Index

Go Top

Go Top

Introduction

Linear Phase(线性相位) FIR Filter

Introduction

When impulse response of  a filter is Finite

       in Length(长度有限), we call this filter a

       Finite Impulse Response (FIR) Filter.    

Difference Equation of FIR Filter (MA Model):

y[n] = b₀x[n] + b₁x[n-1] + ...+ b_Mx[n-M]

Its Frequency Response:

H(Ω) = b₀ + b₁ e ^-jΩ + ...+ b_Me ^-jMΩ

      Its Transfer Function:

H(z) = b₀ + b₁z ^-1 + ...+ b_Mz ^-M

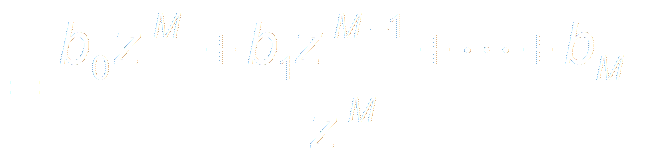
All poles within Unit Circle, system Stable! !

When b_m = b_M-m , m=0,1,2, ..., M

H(Ω) = b₀ + b₁ e ^-jΩ +...+ b₁e ^-j(M-1)Ω + b₀e ^-jMΩ

When b_m = -b_M-m , m = 0,1,2, ..., M

H(Ω) = b₀ + b₁ e ^-jΩ +...+b₁e ^-j(M-1)Ω - b₀e ^-jMΩ

   Symmetric(对称的) Impulse Response

       brings Linear Phase Response

      M-Term Moving Average Filters

         h[n]  = M ^-1( δ[n] + δ[n-1] + ... + δ[n-(M-1)] )

H(z) = M ^-1(1 + z ^-1 + ... + z ^-(M-1))

   H(Ω) = M ^-1(1 + e ^-jΩ + ...+ e ^-j(M-1)Ω)

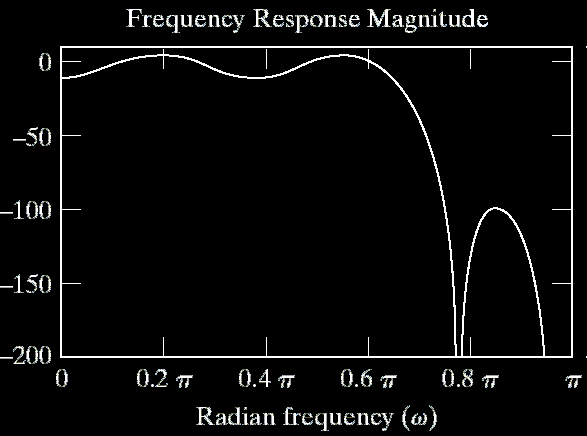
Impulse Response of 5-Term MA Filter

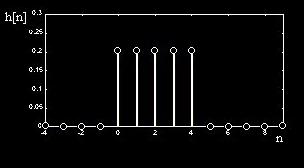
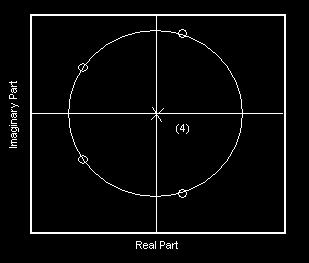
Pole-Zero Plot of 5-Term MA Filter

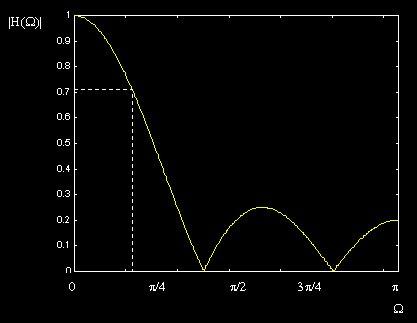
         Filter Shape                  Phase Response

Linear Phase FIR Filter

      Filter Frequency Response:

H(Ω) = |H(Ω)| ÐΦ(Ω)

A.       Φ(Ω) = -DΩ

      Filter Phase Response is a Line

       passing through origin原点 (0,0).

D  = - Φ(Ω)/ Ω Phase Delay相时延

      When  the input x[n] is a single sinusoidal,

x[n] = A cos(nΩ + Φ_x)

Output of the Linear Phase Filter is:

y[n] = AG cos[nΩ + Φ(Ω) + Φ_x]

  = AG cos[ (n -D) Ω + Φ_x ]

Thus if n = D,  all sinusoidal signals have the

       same Zero Phase Shift. Phase of input, of

       any frequency, is preserved保持 without any

       distortion畸变.

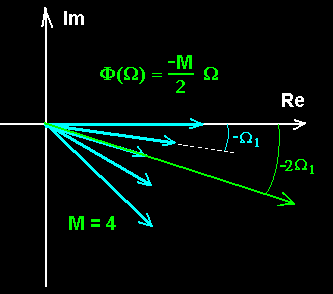
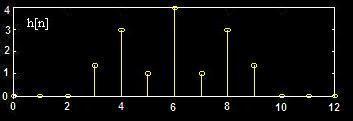
Even Symmetry偶对称 Impulse Response

      gives fixed Phase Delay Linear Phase Filter.

h[n] = h[M-n]     ==>      Φ(Ω) = - (M/2)Ω

B.       Φ(Ω) = Φ₀ - D Ω

     Filter Phase Response is a Line

       passing through point (0, Φ₀).

Group Delay群时延

     When  the input x[n] is a single sinusoidal,

x[n] = A cos(nΩ + Φ_x)

     Output of the Linear Phase Filter is:

y[n] = AG cos[nΩ + Φ(Ω) + Φ_x]

  = AG cos[ (n-D) Ω + Φ_x + Φ₀ ]

Thus if  n = D,  all sinusoidal signals have the

       same Φ₀ Phase Shift.  Phases of inputs, of

       any frequency, are preserved with fixed shift

Φ₀.

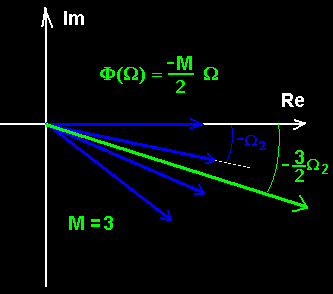
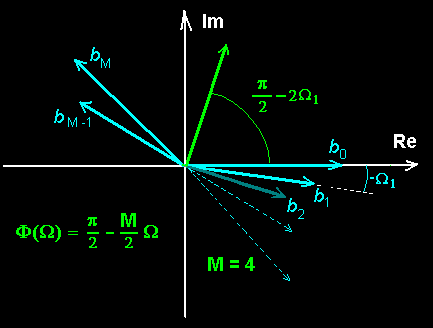
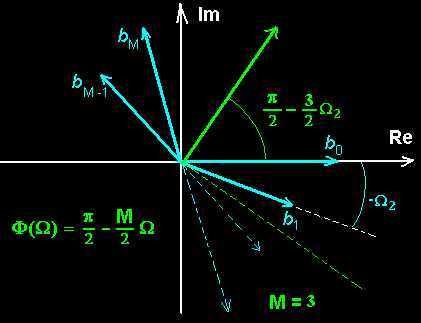
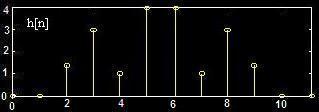
Odd Symmetry奇对称 Impulse Response

       gives fixed Group Delay Linear Phase Filter.

   h[n] = -h[M-n]      ==>   Φ(Ω) = π/2 - (M/2)Ω

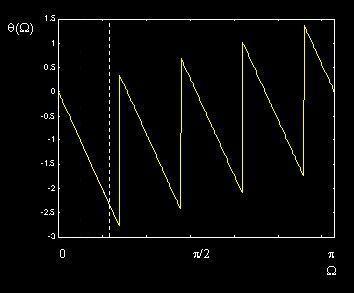
C.   Phase Distortion:  Φ(Ω) = f (Ω)

Group Delay:

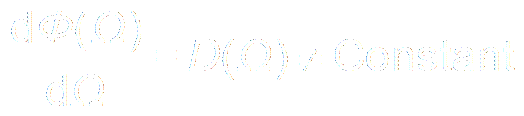
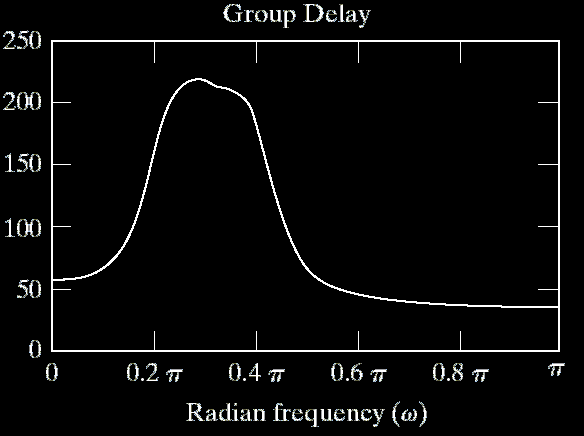
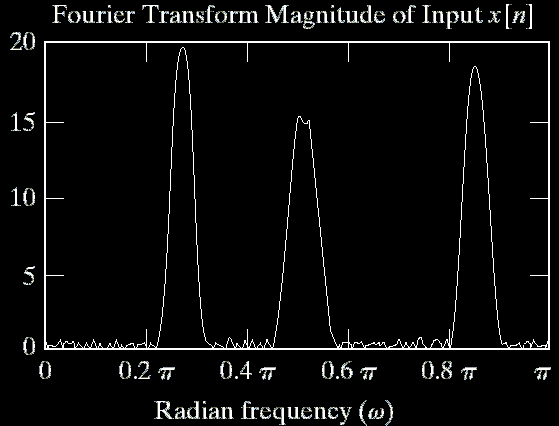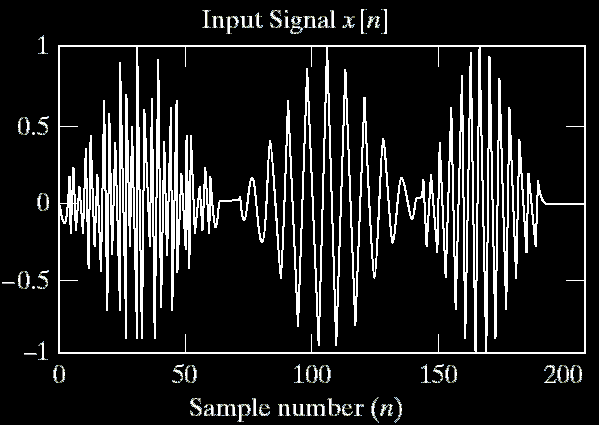
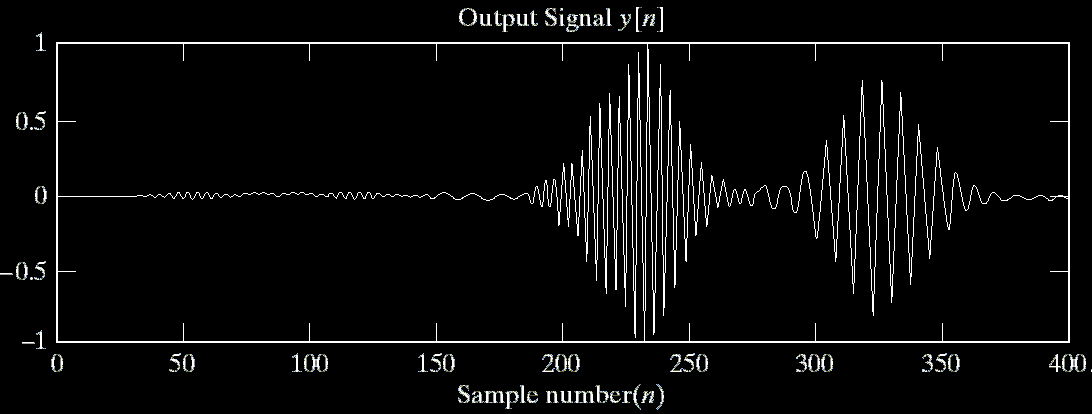
Linear Phase Filter Summary

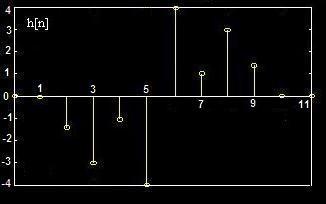
	h[n]	Φ(Ω)
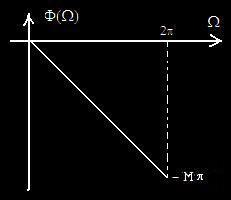
		Fixed Phase Delay: M/2
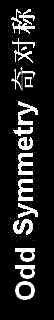
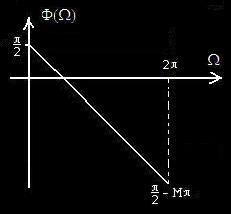
		Fixed Group Delay: M/2