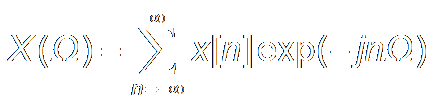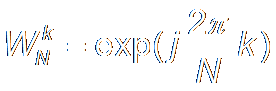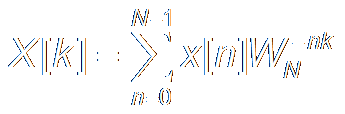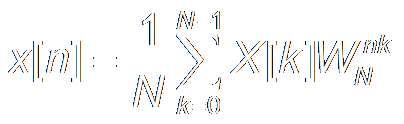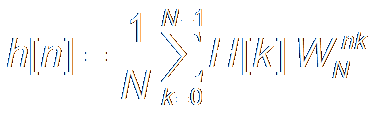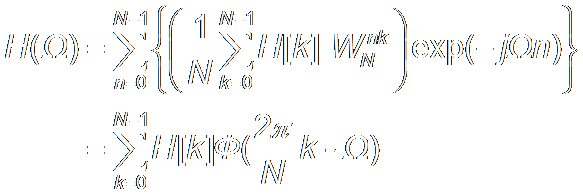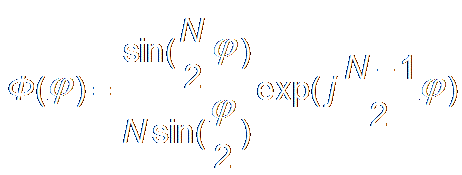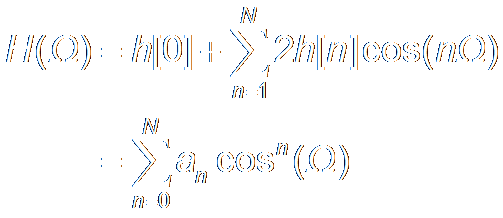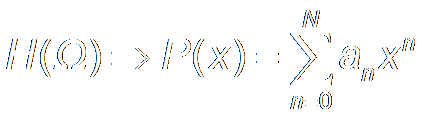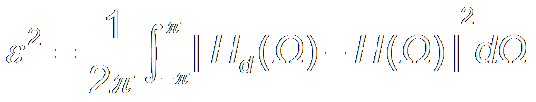Go Top

Discrete Fourier Transform

离散傅立叶变换

Frequency Response Sampling Design频率响应采样设计法

Optimal FIR Filter Approximation

FIR滤波器的最佳逼近

Discrete Fourier Transform

离散傅立叶变换

    Discrete Time Fourier Transform (DTFT):

    In Practice:

           x[n]  is Finite in Time;

            Ω    is not Necessarily Continuous

                    all the time

    If Finite Spectrum Resolution is Acceptable,

    Discrete Fourier Transform (DFT) is used.

     where k = 0, 2, ..., N-1.

     Set:

     Then DFT of Finite Sample Series, x[n], is:

       Inverse DFT (IDFT) is:

Frequency Response Sampling Design频率响应采样设计法

   Idea:

   IDFT of a Filter Frequency Response:

   If H[k] is sampled from the Frequency

   Response of an Ideal Filter Shape H_d(Ω):

              H[k] = H_d(2πk/N),   k = 0, 1, 2, ..., N-1

   h[n] is Ideal, at least on Sampled Frequencies.

   Evaluation:

              H(2πk/N) = H[k] = H_d(2πk/N)

       The Bigger N is,  The Smoother H(Ω) is,

                 The Less Error we have.

   Construct H[k]

         H[k] = H_k exp(jθ_k)

      Even Symmetric Impulse Response:

         θ_k= -kπ   ;   [ Φ(Ω)= -Ω M/2 ]

      Odd Symmetric Impulse Response:

         θ_k= π/2 - kπ ;  [ Φ(Ω)= π/2 - Ω M/2 ]

Optimal FIR Filter Approximation

FIR滤波器的最佳逼近

       Weighted Approximation Error:

            E(Ω) = W(Ω) [H_d(Ω) - H(Ω)]

     Idea:

           To minimize max|E(Ω)| (一致逼近)

           Linear Phase FIR Filter

           (Even Symmetric Impulse Response):

                Set x=cos(Ω),

\                                    

   Equi-ripple Theorem:

      Given P(x) is a r-order Polynomial,

      The  maximum of Weighted

      Approximation Error,

            E_p(x) = W_p(x) [ D_p(x) - P(x) ]

      is minimized when P(x) has (r+2)

      Alternative Points at least, where

            x₁ < x₂ < ... < x_r+2

            P(x_i) = -P(x_i+1) = ?max|E_p(x)|

      Windowed Design is not Optimal

           by means of Square Mean Error:

        is minimized.

      Optimal FIR Filter Approximation:

          (Parks-McClellan Method)

       A.V.奥本海姆, R.W.谢弗,  J.R巴克

   《离散时间信号处理》第二版 

    西安交通大学出版社 2002, Page 400