Index
	Go Top
Go Top

Region Of Convergence (ROC)

收敛域

System Stability系统稳定性

Homework:

         p225: 6.28,  p229: 6.35

Region of Convergence (ROC)

收敛域

x[n]	d [n]	u [n]	b^n u[n]	n u[n]
X(z)	1
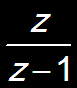
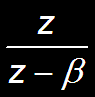
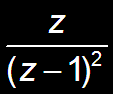
ROC	All z	|z|>1	|z|>b	|z|>1

 Geometric几何(Power幂级数) Series序列:

Convergence Condition收敛条件:

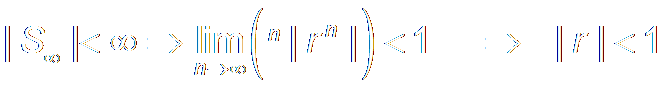
ROC of Finite Sample Series

有限样本序列

z ≠ 0 and/or  z ≠ ∞ Q1: Y?

ROC of Right Side Series右边序列

Z Transform:
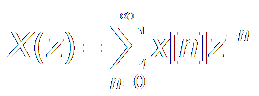
Convergence Condition:

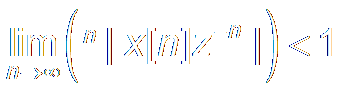
ROC of Left Side Series左边序列

Z Transform:
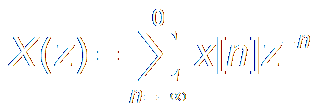
Convergence Condition:

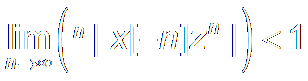
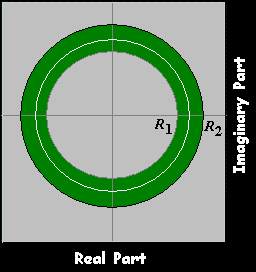
ROC of Double Side Series双边序列

where R₁, R₂ must satisfy: R₁<R₂

Q: Deduce推导 the Z transform  of  -u[-n-1],

then find its ROC.

System Stability系统稳定性

The Poles and Zeros极点和零点

From Transfer Function传递函数

Zeros零点 are Roots  of

b₀z^N + b₁z^N-1 + b₂z^N-2 + ··?+ b_Mz^N-M = 0

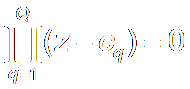
Zeros: {c_q ; q=1,2, ··? Q } ,

Q is the highest order of numerator分子.

 Poles极点 are Roots of

a₀z^N + a₁z^N-1 + a₂z^N-2 + ··?+ a_N = 0

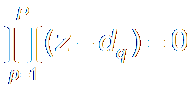
       Poles: {d_p ; n=1,2, ··? P}

P is the highest order of denominator分母.

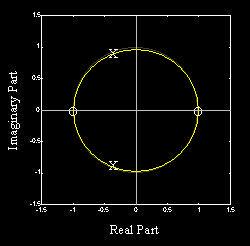
Pole-Zero Plot 零极点图  "X":   Poles极点 "O":  Zeros零点

Stability稳定性& ROC

For Discrete Time, Linear Time Invariant (LTI)

       system h[n],

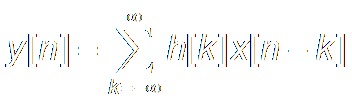
         When |x[n]|<B , if |y[n]|<∞, the system is Stable.

         It is equivalent to: The system is Absolutely

Summable. 绝对可和

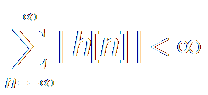
         It is the same thing of

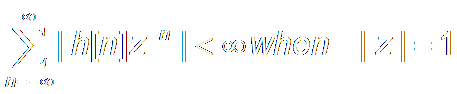
         This means: H(z) is Convergent on the unit circle.

Conclusion:

              If a LTI system is stable, the ROC of its

H(z)  must include unit circle.

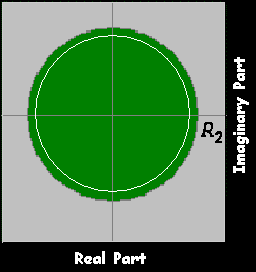
Left Side                     Right  Side                  Double Sides

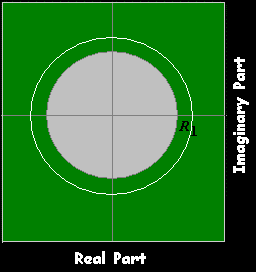
|z|<R₂ ，R₂≥1 |z|>R₁ ，R₁≤1 R₁<|z|<R₂ ，R₁≤1≤ R₂

Poles to Stability极点与稳定性

If Any Pole lies outside the unit circle,

           System is Unstable 不稳定.

       If the Outermost最远的 Pole is on the unit circle,

System is Marginally Stable边缘稳定.

Only when All Poles are inside the unit circle,

           System is Stable稳定.

Stability Region for Poles

极点稳定域

The Partial Fraction Expansion of X(z):

部分分式展开

  If there is a pole outside unit circle,

         that means  |β_k|>1, then the corresponding

sub-system:

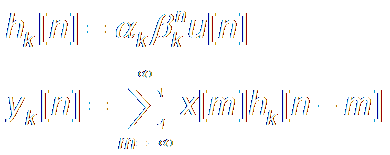
   |x[n]|<B , |y_k[n]| →∞, sub-system Not stable,

Thus the whole system is Unstable.

Responses of Stable System

稳定系统的响应

常数

h[n]: Impulse Response;   s[n]: Step Response

冲激响应 阶跃响应

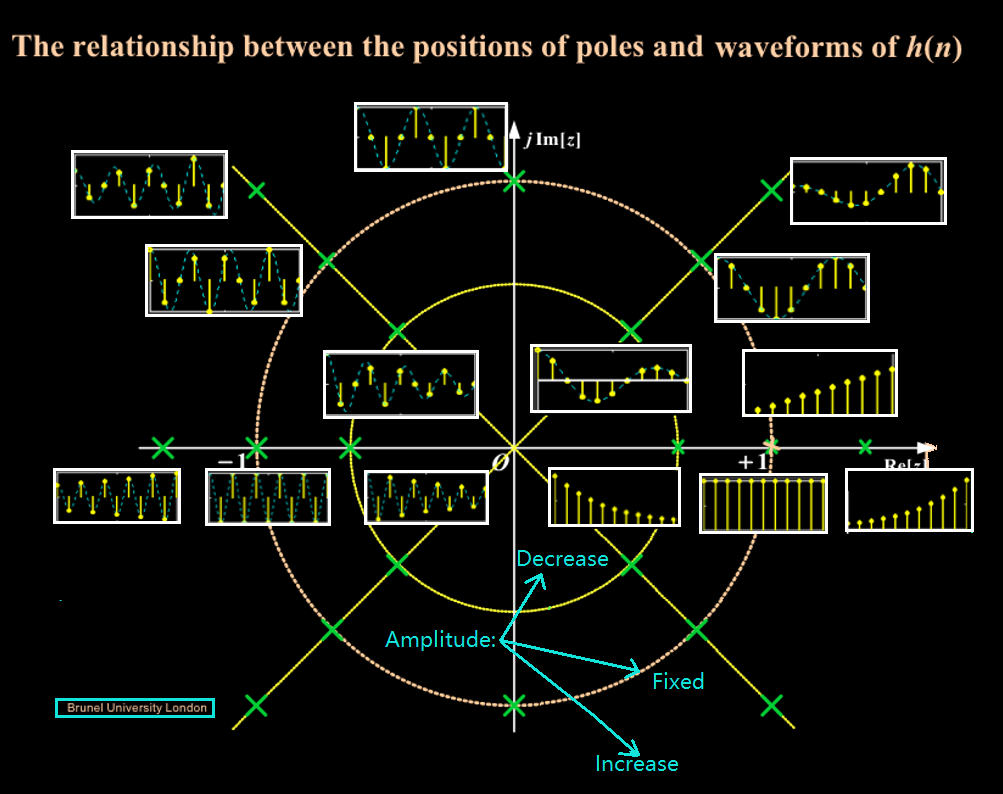
         Page 213 Fig6.24;     Page 220 Fig6.26.

The Closer the poles are to the origin,

         the Faster the system reach its Steady State.

If poles are on the Left half of Z plane,

         the Responses alternate交替 between

         Positive and Negative sample by sample.

The Closer the zeros are to the poles,

         the Greater the response being Attenuated衰减.