|
Z
Transform Z变换
Properties性质 of Z Transform
Transfer Function传递函数
Homework:
P222: 6.6 P22: 6.11
Z Transform Z变换
Definition of Z Transform Z变换定义
x[n]
X(z)
Time Domain时域
Z Domain Z域
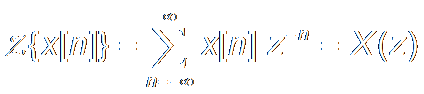
Z{·} denotes代表 Z transform Operation
z is a Complex Variant复变量.
Z Transforms of Basic Series
基本序列的Z变换
|
x[n]
|
d [n]
|
u [n]
|
b
n u[n]
|
n u[n]
|
|
X(z)
|
1
|
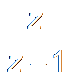
|
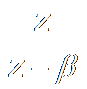
|
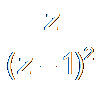
|
Transfer Function传递函数
Definition定义
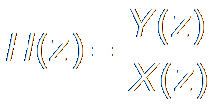
Transfer Functions of Typical Systems
典型系统的传递函数
Z{
x[ n-k ]} = z -k X(z)
MA Model滑动平均模型
y[n] = b0x[n]
+ b1x[n-1] + L + bMx[n-M]
H(z) = b0 + b1z-1
+ L
+ bMz-M
ARMA
Model 自回归滑动平均模型
a0y[n]
+ a1y[n-1] + L + aNy[n-N]
= b0x[n] + b1x[n-1]
+ L
+ bMx[n-M]
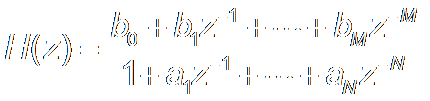
System Combination系统组合
Cascade Connection串联
H(z) = H1(z)H2(z)
Parallel Connection并联
H(z) = H1(z) + H2(z)
Read
book page 181 Fig6.6 & page 183 Fig6.8
Properties性质 of Z Transform
Basic
Properties基本性质
1.
Linearity线性
Z{a
x1[n]+b x2[n]} = a X1(z)+b
X2(z)
2. Time Shift时移
Z{
x[ n-k ]} = z -k X(z)
-----------------------------------------------------------
Q: Given Z transform of x[n]
as X(z),
deduce推导 the Z transform of
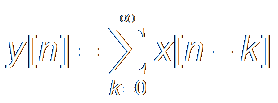
----------------------------------------------------------
3. Time Reverse时间倒置
Z{
x[ - n ]} = X(z -1 )
4. Time Upsampling时间扩展
Z{
x[ n/k ]} = X(z k )
where x[ n/k ]=0 if n≠0,
k, 2k,...
k is integer number.
5. Zooming缩放
Z{ an x[n]} =
X(a-1z)
6. Conjugacy共轭性
Z{ x*[n]} =
X*( z* )
7. Differential微分
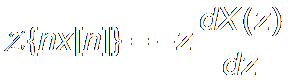
Law of
Convolution卷积定律
Y(z)
= X(z) H(z), y[n] = x[n]*h[n]
Z{
x[n]*h[n] } = X(z) H(z)
Initial Value
Theorem初值定理
If x[n] is a casual series, x[n]=0 for n<0,
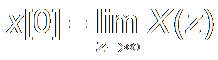
|