|
Filtering and
Filter Features特性
Difference
Equations差分方程
Impulse Response冲激响应
Step Response阶跃响应
Filtering and
Filter Features特性
Filtering = Making Selection
+ Amplification or Attenuation
放大
衰减
Cut-off
Frequency截止频率
The
frequency where filter makes a -3 dB
attenuation衰减, comparing with the
maximum gain增益.
20log(GC /GM)
= -3 dB or GC /GM = 0.707
Bandwidth带宽
Distance between frequencies where
signal can pass or being blocked. 阻止
Roll-off滚降
Steeper Roll-off, Higher Order, Better
Quality.
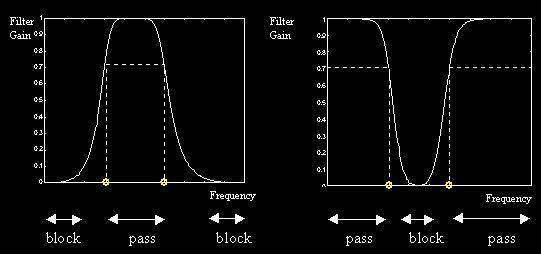
Low Pass
Filter High
Pass Filter
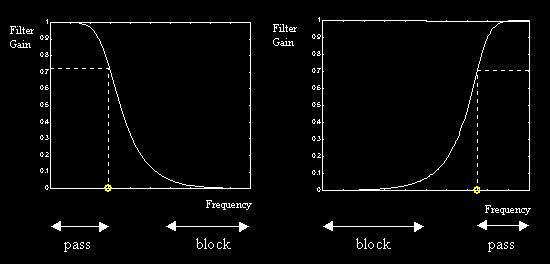
Band Pass
Filter Band Stop
Filter
The Law of Superposition叠加定律
For system y = f
(x), if y1 + y2 = f
( x1 + x2 ),
the system is Linear, can be Superposed.
Time Invariant System时不变系统
For y [
n ] = f ( x [ n ] ),
if y [ n - K ] = f ( x [ n - K ]
),
the system is Time Invariant.
Causal System因果系统
No
Future Data Involved!
Difference
Equation 差分方程
MA (Moving Average滑动平均) Model
y[n] = b0x[n]
+ b1x[n-1] + L + bMx[n-M]
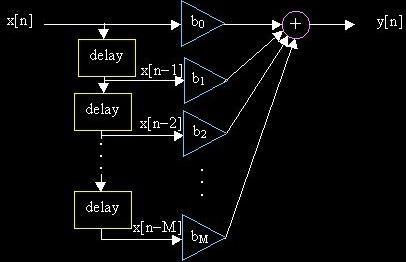
Non-Recursive非迭代的
Linear, Time Invariant,
Causal System.
线性时不变因果系统
ARMA Model
(Auto Regressive Moving Average)
自回归
滑动平均
a0y[n] + a1y[n-1]
+ L + aNy[n-N]
= b0x[n] + b1x[n-1]
+ L + bMx[n-M]
{ak ;
k =0,1,2, ... ,N } : AR Coefficients.
{bk ; k =0,1,2, ... ,M
} : MA Coefficients.
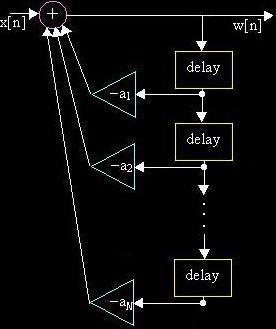
Direct
Form直型1:
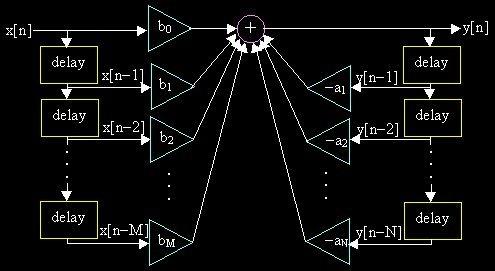
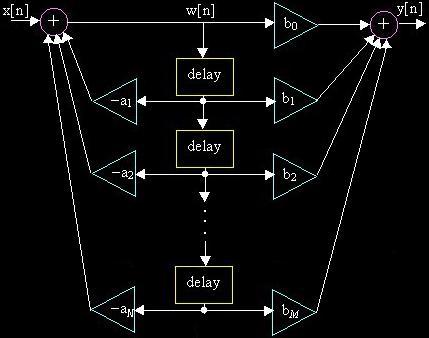
Direct Form直型2:
w[n] = x[n]
- a1w[n-1] - L - aNw[n-N ]
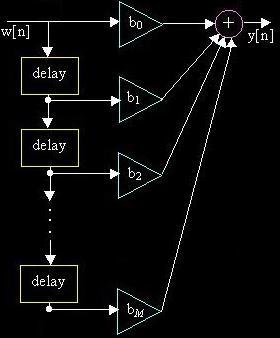
y[n]
= b0w[n] + b1w[n-1]
+ L + bMw[n-M
]
  - -
ARMA Model is Recursive迭代的
Linear, Time Invariant,
Causal System.
线性时不变因果系统
Impulse
Response冲激响应
The response of filter to the impulse input.
x [n] → d [n] ;
y [n] → h [n]
y[n] = b0x[n]
+ b1x[n-1] + L + bMx[n-M]
h[n] = b0 d [n] + b1 d [n-1] + L + bM d [n-M ]
a0y[n] + a1y[n-1]
+ L
+ aNy[n-N]
= b0x[n] + b1x[n-1]
+L
+ bMx[n-M]
h[n]= -a1h[n-1]
- L
-aNh[n-N ]
+b0d [n] + b1d [n-1] + L + bMd [n-M ]
FIR
(Finite
Impulse Response)有限冲激响应
IIR (Infinite
Impulse Response)无限冲激响应
Step
Response阶跃响应
The response of a filter to the
step input.
x
[n] → u [n] ;
y [n] → s [n]
y[n] = b0x[n]
+ b1x[n-1] + L + bMx[n-M]
s[n] = b0 u [n] + b1
u [n-1] + L + bM u [n-M ]
a0y[n] + a1y[n-1]
+ L
+ aNy[n-N]
= b0x[n] + b1x[n-1]
+ L
+ bMx[n-M]
s[n]= -a1s[n-1]
- L
-aNs[n-N ]
+b0 u [n] + b1
u [n-1] + L + bM u [n-M ]
Sum of Impulse Responses.
|
Input
|
d [n]
|
u [n]
=d [n]+d [n-1]+L+d [0]
|
|
Output
|
h [n]
|
s [n] =h [n]+h
[n-1]+L+h [0]
For Linear System Only.
|
y=x^2
|