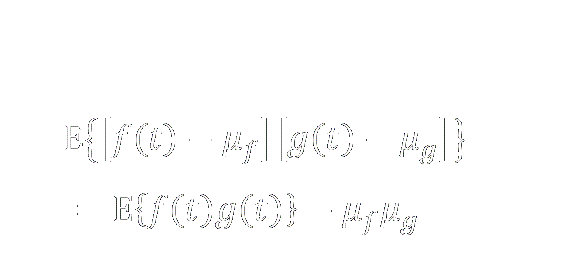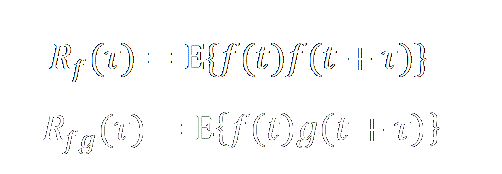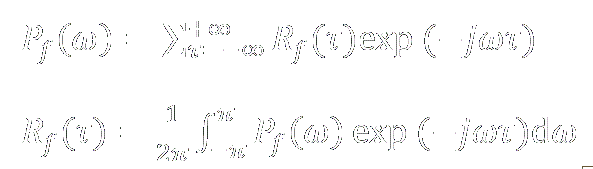|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Stochastic Variable 随机变量
Stochastic Process 随机过程
数学期望
方差与协方差
自相关与互相关
维纳-辛钦定理
Stochastic (Random) Variable 随机 变量
Random Variable x: If W is a probability space, a random variable x on W is a measurable function f to a measurable space D which is frequently taken to be the real number.
Probability Distribution Function 概率 分布 函数
Probability Density Function 概率 密度 函数
Weight ↔ Weight Density
Stochastic Process 随机过程
Undetermined不确定 ≠ Unpredictable不可知
A Time-indexed collection of Random Variables (随机变量RV), each of which is defined on the same Probability Space(概率空间) "W" and takes values on the same Codomain(值域) D (often the real R). { f(t): W → D } , t ∈ T T : Index Set(下标集)
Stochastic Process (SP)
Probability Distribution & Density:
For any {t1, t2, ..., tn}, denote f(tk) as Xk: If X1 doesn't correlate with X2, then we have Independent SP(独立随机过程)
For any {t1 < t2 < ...< tn }, If (Xk+1 - Xk) doesn't correlate with (Xk+r+1 - Xk+r) , then we have Independent Increment Process(独立增量过程)
If Independent SP has Pt1 (x,t) = Pt2 (x,t) = ... = Ptn (x,t) then we have Independent Identical Distribution (IID) Process(独立同分布过程)
If all n-Dimensional Probability Distributions Pt1,t2,...,tn (x,t) are all same, (n = 1,2,3,...), then we have (Strict-Sense) Stationary SP (狭义平稳随机过程)
If E{ f(t) } and E{ f(t) f(t+t) } don't change with time t, then we have Wide-Sense Stationary SP (广义平稳随机过程)
Discrete SP: t = {t1, t2, t3, ..., tn}, Discrete Set(离散集) Continuous SP: t ∈ R, Continuous Set(连续集)
IF tk = kTs , (k∈ Z), then we have Random Sequence (随机序列)
IF f(t)=V is a Vector Variable, then we have Vector SP(矢量随机过程)
Mathematic Expectation数学期望 --- Mean 均值
For a SP:
For a Finite State Random Event:
Time Average
Ergodic Process (各态历经过程): One Sample can represent the whole Process.
Variance & Covariance
Auto-Correlation 自相关 & Cross-Correlation 互相关
Wiener-Khinchin Theorem
For any SP, Power Spectral Density功率谱密度 and Autocorrelation自相关 are related with Fourier Transform :
|
|