|
Butterworth IIR LPF Design
Chebyshev IIR LPF Design
Filter Shape
Transformation
Homework
p431: 10.8, p432: 10.16
Butterworth IIR LPF Design

Given
Features: { fpass , fstop
, dp, ds, fs }
Impulse Invariance Method
a. ωp = 2π fpass
; ωs = 2π fstop
;
b. Solve Equation Set:

for N and ωc
c. Compute Poles:
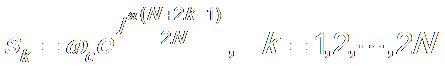
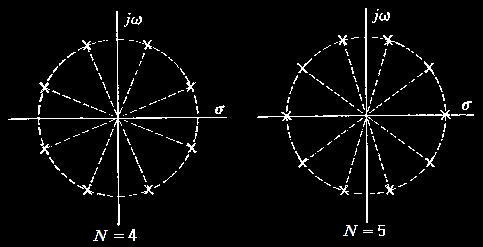
d. Transfer Function:
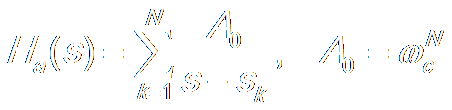
 ?/span> ?/span> ?/span> ?/span> ?/span> ?/span>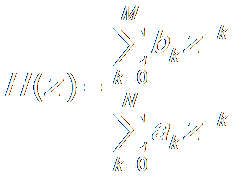
e. Compare |H(Ω)| to | H(ω)|
Bilinear Transform Method
a.
Ωp = 2π fpass /
fs ; Ωs = 2π
fstop /fs;
b. ωp = 2fs tan(Ωp)
; ωs = 2fs
tan(Ωs) ;
c. Determine Order N and ωc by:
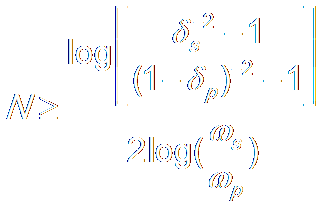
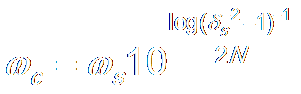
d.
Use Bilinear Transform to get h[n]
|
H(s)
→
|
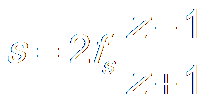
|
→
|
H(z)
→ |H(Ω)|
|
e. Compare |H(Ω)|
to | H(ω)|
Butterworth Filter Shape vs Order
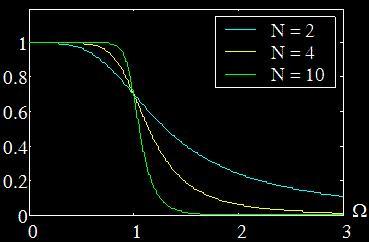
Chebyshev IIR LPF Design
Given
Features: { fpass , fstop
, dp, ds, fs }
Impulse Invariance Method
a. ωp = 2π fpass
; ωs = 2π fstop
;
b. 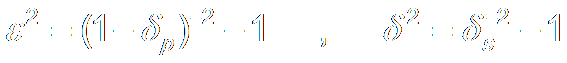
c. Determine Order N by:
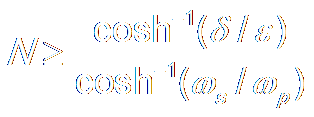
d. Compute Poles From
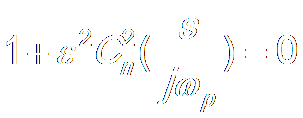
e. Build Ha(s)

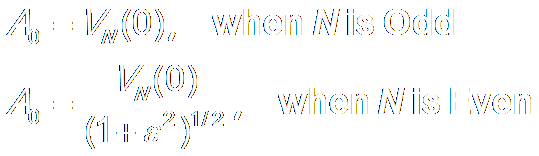
f.
Transfer Function:
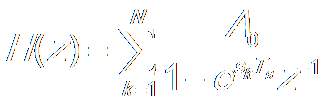 ?/span> ?/span>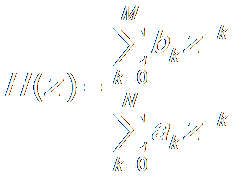
g.
Compare |H(Ω)| to | H(ω)|
Bilinear
Transform Method
a.
Ωp = 2π fpass / fs
; Ωs = 2π fstop
/fs;
b. ωp = 2fs tan(Ωp)
; ωs = 2fs
tan(Ωs) ;
c. ε2 = (1-dp)-2 - 1
d. Determine Order N by:
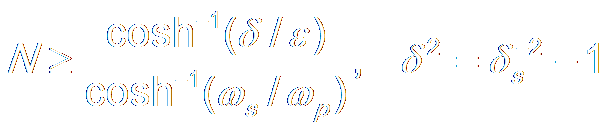
e. Use Bilinear Transform get h[n]
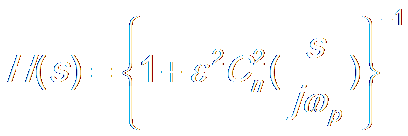
|
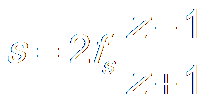
|
→
|
H(z) → |H(Ω)|
|
f. Compare |H(Ω)|
to | H(ω)|
Chebyshev
Type I
Filter Shape vs Order
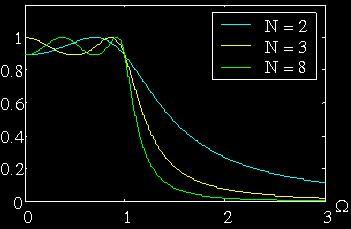
Filter Shape Transformation
S
Domain
Low Pass → Low Pass

Low Pass → High Pass
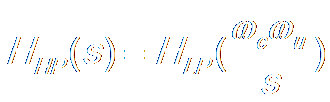
Low Pass → Band Pass
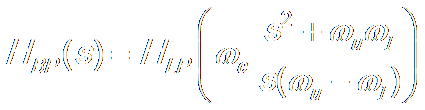
Low Pass → Band
Stop
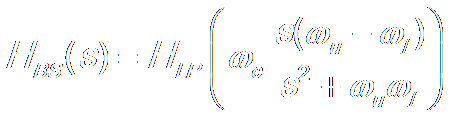
z
Domain
Low Pass → Low Pass
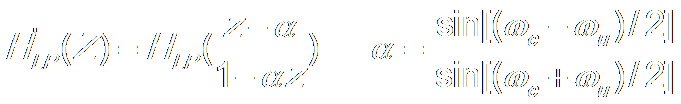
Low Pass → High Pass
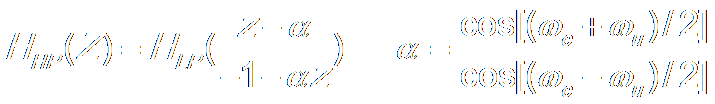
|
Low Pass →
Band Pass
|
|
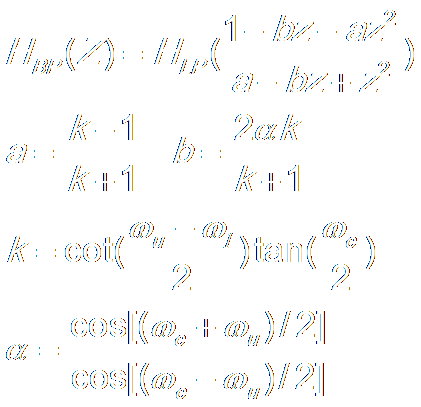
|
|
Low Pass → Band Pass
|
|
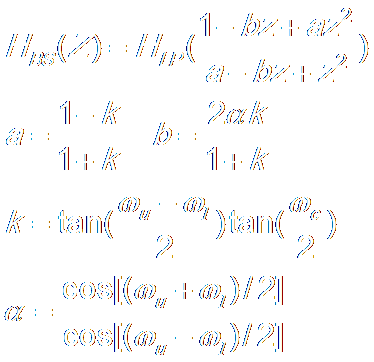
|
|